Symmetric Singular Matrix Example | The entries of a symmetric matrix are symmetric with respect to the main diagonal. Symmetric matrix is a square matrix which is equal to its transpose. A regular matrix is a square matrix that has an inverse. The matrix $s$ is defined as the following: So efficiently creating an symmetric matrix is just a subset of the efficient matrix definition problem.
Every real symmetric matrix is diagonalizable. For example, we have a 3×2 matrix, that's because the number of rows here is equal to 3 and the number of columns is equal to 2. A symmetric matrix is a square matrix that verifies So a symmetric matrix must be a square matrix. One important example of applying a function to a matrix is powering.

Nevertheless, each algorithm has an extension for complex matrices. Diagonal matrices play a crucial role in matrix theory. However, for certain values there will be a solution the conjugate gradient method is suitable for symmetric positive definite systems, always converging to a solution (though the convergence may be slow). Symmetric matrix can be obtain by changing row to column and column to row. In the dense case the simplest way is to just sum the. So a symmetric matrix must be a square matrix. Here is a larger example, when the u's and the v's are just columns of the identity matrix. The matrix $s$ is defined as the following: For example, if we take a matrix x, whose elements of the first column are zero. It is analogous to the qr algorithm for symmetric matrices. 45.2 algorithms for the singular value decomposition. For example, we have a matrix contains the return. This formularization has some interesting implications.
Nevertheless, each algorithm has an extension for complex matrices. Definition of symmetric matrix, from the stat trek dictionary of statistical terms and concepts. Logic to check symmetric matrix. A symmetric matrix is a square matrix that verifies A regular matrix is a square matrix that has an inverse.

In the dense case the simplest way is to just sum the. Singular vectors & singular values. For examples illustrating svd, see chapter 5.6. Properties of real symmetric matrices. Register free for online tutoring session to clear your doubts. In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. $s=aa^{\top}$ and is hence a symmetric positive semidefinite matrix. 45.2 algorithms for the singular value decomposition. So efficiently creating an symmetric matrix is just a subset of the efficient matrix definition problem. We prove all symmetric matrices is a subspace of the vector space of all n by n matrices. Two examples of symmetric matrices appear below. (i) p −1ap = d, where d a diagonal matrix. O(n x n) auxiliary space :
Properties of real symmetric matrices. So a symmetric matrix must be a square matrix. We prove all symmetric matrices is a subspace of the vector space of all n by n matrices. In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Every real symmetric matrix is diagonalizable.
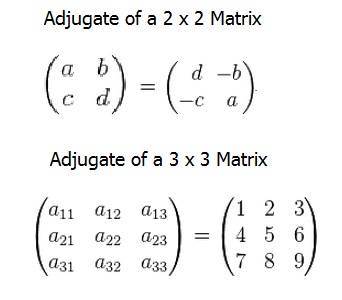
Symmetric matrices, such as correlation matrices and covariance matrices, are quite common in multivariate analysis, and we shall come across them example 21.11. You can easily create symmetric matrix either by. So efficiently creating an symmetric matrix is just a subset of the efficient matrix definition problem. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So the computations are easy, but keep your eye the singular values σi of a are the square roots of the eigenvalues λi of s = ata. Two examples of symmetric matrices appear below. Nevertheless, each algorithm has an extension for complex matrices. A symmetric matrix is a square matrix that verifies The matrix $s$ is defined as the following: For example, the following matrix is singular: Logic to check symmetric matrix. Every real symmetric matrix is diagonalizable. Is positive definite matrix 21.
Covariance matrices are not only symmetric but they are also positive semidefinite singular matrix example. For example, the following matrix is singular:
Symmetric Singular Matrix Example: Symmetric matrix can be obtain by changing row to column and column to row.